В сокращенном виде статья опубликована в журнале "Открытые системы", 2002, №3

DVM-ПОДХОД
К РАЗРАБОТКЕ ПАРАЛЛЕЛЬНЫХ ПРОГРАММ ДЛЯ ВЫЧИСЛИТЕЛЬНЫХ КЛАСТЕРОВ И СЕТЕЙ 

Н.А. Коновалов,

В.А. Крюков

Институт прикладной математики им. М.В. Келдыша РАН

e-mail:  konov@keldysh.ru,  krukov@keldysh.ru,

 

 Аннотация.

 DVM-подход к разработке параллельных программ отличается, прежде всего, использованием новой модели программирования – модели параллелизма по данным и управлению. Базирующаяся на этом подходе DVM­-система предоставляет программисту языки программирования C-DVM и Fortran-DVM, позволяющие ему  написать один вариант программы и для последовательного и для параллельного выполнения. Эта программа, помимо описания алгоритма обычными средствами языков Си или Фортран, содержит спецификации параллелизма - правила параллельного выполнения этого алгоритма. Эти правила оформляются синтаксически таким образом, что они являются «невидимыми» для стандартных компиляторов с последовательных языков Си и Фортран и не препятствуют выполнению и отладке DVM-программы на рабочих станциях как обычной последовательной программы.

 

1. Введение

С 1992 года, когда многопроцессорные системы с распределенной памятью (мультикомпьютеры) стали самыми производительными вычислительными системами, резко возрос интерес к проблеме разработки для них параллельных прикладных программ. К этому моменту уже было ясно, что трудоемкость разработки  прикладных программ для мультикомпьютеров является главным препятствием для их широкого внедрения. За прошедший с тех пор период предложено много различных подходов к разработке параллельных программ, созданы десятки различных языков параллельного программирования и множество различных инструментальных средств.

Главным фактором, определяющим тот или иной подход, является модель программирования. Модель программирования нельзя путать с моделью выполнения параллельной программы. Модель программирования может быть очень близка к модели выполнения, а может отличаться от нее значительно.

Имеются две основные модели параллельного выполнения программы на многопроцессорных ЭВМ – модель передачи сообщений и модель общей памяти. 

В первой модели параллельная программа представляет собой систему процессов, взаимодействующих посредством передачи сообщений. Эта модель может быть использована на любых многопроцессорных ЭВМ.

Во второй модели параллельная программа представляет собой систему нитей, взаимодействующих посредством общих переменных и примитивов синхронизации. Нить (по-английски ”thread”) – это легковесный процесс, имеющий с другими нитями общие ресурсы, включая общую оперативную память. Эта модель может использоваться только на многопроцессорных ЭВМ с общей памятью или с DSM (Distributed Shared Memory - распределенная общая память).

Можно выбрать в качестве модели  программирования одну из этих моделей выполнения (примерами являются, Фортран+MPI, Си+Pthreads, Occam). Однако такая низкоуровневая модель непривычна и неудобна для программистов, разрабатывающих вычислительные программы. Она заставляет его иметь дело с параллельными процессами и низкоуровневыми примитивами передачи сообщений или синхронизации. И, главное, программист должен распределять вычисления  (а в модели передачи сообщений еще и данные) между процессами.

Поэтому вполне естественно, что прикладной программист хотел бы иметь дело с высокоуровневой моделью программирования. Такая модель должна позволять ему по-прежнему описывать алгоритм в терминах массива целиком (как он привык делать на последовательных ЭВМ), а  не требовать от него манипулирования локальными частями массива, размер которых зависит от числа используемых процессоров.

Примером такой высокоуровневой модели является модель последовательного программирования. Мечта всех прикладных программистов - получить инструмент, автоматически преобразующий его последовательную программу в параллельную программу. К сожалению, для систем с распределенной памятью такое автоматическое распараллеливание обеспечить не удается в силу следующих причин.

Во-первых, поскольку взаимодействие процессоров через коммуникационную систему требует значительного времени (латентность – время самого простого взаимодействия – велика по сравнению со временем выполнения одной машинной команды), то вычислительная работа должна распределяться между процессорами крупными порциями.

Совсем другая ситуация была на векторных машинах и на многопроцессорных системах с общей памятью (мультипроцессорах), где автоматическое распараллеливание программ на языке Фортран реально использовалось и давало хорошие результаты. Для автоматического распараллеливания на векторных машинах (векторизации) достаточно было проанализировать на предмет возможности параллельного выполнения (замены на векторные операции) только самые внутренние циклы программы. В случае мультипроцессоров приходилось уже анализировать объемлющие циклы для нахождения более крупных порций работы, распределяемых между процессорами. 

Укрупнение распределяемых порций работы требует анализа более крупных фрагментов программы, обычно включающих в себя вызовы различных процедур. Это, в свою очередь, требует сложного межпроцедурного анализа.  Поскольку в реальных программах на языке Фортран могут использоваться конструкции, статический анализ которых принципиально невозможен  (например, косвенная индексация элементов массивов), то с увеличением порций распределяемой работы увеличивается вероятность того, что распараллеливатель откажется распараллеливать те конструкции, которые на самом деле допускают параллельное выполнение.

Во-вторых, в отличие от многопроцессорных ЭВМ с общей памятью,  на системах с  распределенной  памятью необходимо произвести не только распределение вычислений, но и  распределение  данных, а также обеспечить на каждом процессоре доступ к удаленным данным – данным, расположенным на других процессорах. Для обеспечения эффективного доступа к удаленным данным недостаточно просто обнаруживать факт наличия зависимости по данным в цикле или между разными циклами, а требуется определить точно тот сегмент данных, который должен быть переслан с одного процессора на другой.

В третьих, распределение вычислений и данных должно быть произведено согласованно.

Несогласованность распределения вычислений и данных приведет,  вероятнее всего, к тому, что параллельная программа будет выполняться гораздо медленнее последовательной.  Если на системе с общей памятью распараллелить один цикл, занимающий 90 процентов времени решения задачи,  то можно рассчитывать на почти десятикратное ускорение  программы, даже если оставшиеся 10 процентов будут выполняться последовательно.  На системе с распределенной памятью распараллеливание этого цикла без учета последовательной части может вызвать  не ускорение, а замедление программы, поскольку для выполнения последовательной части  потребуется интенсивный обмен данными между процессорами.

Согласованное распределение вычислений и данных требует тщательного анализа  всей программы, и любая неточность анализа может привести к катастрофическому замедлению выполнения программы.

 

Следует отметить, что если бы программисту все же предоставили бы желанный инструмент, то он столкнулся бы с другой проблемой – проблемой анализа и повышения эффективности выполнения полученной параллельной программы. Поскольку модель программирования очень далека от модели выполнения, то было бы очень трудно объяснить программисту, какие преобразования  программы он должен осуществить для ее эффективного выполнения. 

В модели параллелизма по данным отсутствует понятие процесса и, как следствие, явная передача сообщений  или явная синхронизация. В этой модели данные последовательной программы распределяются программистом по процессорам параллельной машины. Последовательная программа преобразуется компилятором в параллельную программу, выполняющуюся либо в модели передачи сообщений, либо в модели с общей памятью. При этом вычисления распределяются по правилу собственных вычислений: каждый процессор выполняет только вычисления собственных данных, т.е. данных, распределенных на этот процессор.

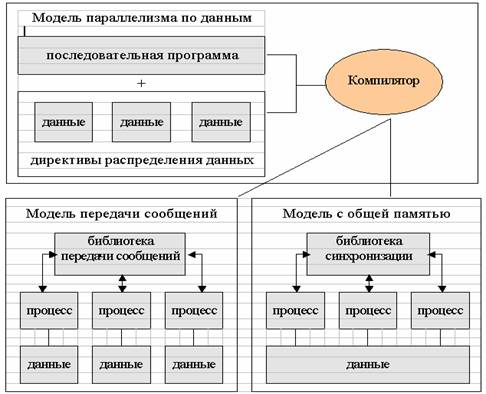
Рисунок 1.  Схема отображения программы в модели параллелизма по данным.

Обобщение и стандартизация моделей параллелизма по данным привели к созданию в 1993 году стандарта HPF (High Performance Fortran [1]) - расширения языка Фортран 90.

Безусловно, по сравнению с MPI язык HPF намного упрощает написание параллельных программ, однако его реализация требует от компилятора очень высокого интеллекта. Конечно, самая сложная часть работы, которая вызывала проблемы при автоматическом распараллеливании – распределение данных – возлагается теперь на программиста. Но, и с оставшейся частью работы  компилятор не всегда способен справиться  без дополнительных подсказок программиста.

Модель параллелизма по управлению возникла как естественная альтернатива явному использованию модели общей памяти при разработке программ для мультипроцессоров. Вместо программирования в терминах нитей  предлагалось расширить языки специальными управляющими конструкциями – параллельными циклами и параллельными секциями, позволяющими, например, легко описать параллельное выполнение нескольких процедур. Создание и уничтожение нитей, распределение между ними витков параллельных циклов или параллельных секций  – все это брал на себя компилятор. Первая попытка стандартизовать такую модель привела к появлению в 1990 году проекта языка PCF Fortran (проект стандарта X3H5). Однако, этот проект [2] тогда не привлек широкого внимания. Возможно, что причиной этого было снижение интереса к мультипроцессорам и всеобщее увлечение мультикомпьютерами и HPF.

Однако, спустя несколько лет ситуация сильно изменилась. Во-первых, успехи в развитии элементной базы сделали очень перспективным и экономически выгодным создавать мультипроцессоры. Во-вторых, надежды на то, что HPF станет фактическим стандартом для разработки вычислительных программ, не оправдались – разработчикам компиляторов не удалось добиться приемлемой эффективности выполнения HPF-программ.

Крупнейшие  производители компьютеров и программного обеспечения  объединили свои усилия и в октябре 1997 года выпустили описание языка OpenMP Fortran [3] – расширение языка Фортран 77. Позже вышли аналогичные  расширения языков Си и  Фортран 90/95.

 

2. Модель параллелизма по данным и управлению

Эта модель, положенная в основу языков параллельного программирования Fortran-DVM [4] и C-DVM [5],  объединяет достоинства модели параллелизма по данным и модели параллелизма по управлению. Базирующаяся на этих языках система разработки параллельных программ (DVM-система [6]) создана в Институте прикладной математики им. М.В. Келдыша РАН.

В отличие от модели параллелизма по данным,  в DVM-системе программист распределяет по процессорам параллельной машины не только данные, но и соответствующие вычисления.

При построении DVM-системы был  использован новый подход, который характеризуется следующими принципами.

1.      Система должна базироваться на высокоуровневой модели выполнения параллельной программы, удобной и понятной для программиста, привыкшего программировать на последовательных языках. Такая модель (DVM-модель) была разработана в 1994 году [4].

2.      Языки параллельного программирования должны представлять собой стандартные языки последовательного программирования, расширенные спецификациями параллелизма. Эти языки должны предлагать программисту модель программирования, достаточно близкую к модели выполнения. Знание программистом модели выполнения его программы и ее близость к модели программирования существенно упрощает для него анализ производительности программы и проведение ее модификаций, направленных на достижение приемлемой эффективности.

3.      Спецификации параллелизма должны быть прозрачными для обычных компиляторов (например, оформляться в виде специальных комментариев). Во-первых, это упрощает внедрение новых параллельных языков, поскольку программист знает, что его программа без каких-либо изменений может выполняться в последовательном режиме на любых ЭВМ. Во-вторых, это позволяет использовать следующий метод поэтапной отладки DVM-программ. На первом этапе программа отлаживается на рабочей станции как последовательная программа, используя обычные методы и средства отладки. На втором этапе программа выполняется на той же рабочей станции в специальном режиме проверки DVM-указаний. На третьем этапе программа может быть выполнена в специальном режиме, когда промежуточные результаты параллельного выполнения сравниваются с эталонными результатами (например, результатами последовательного выполнения).

4.      Основная работа по реализации модели выполнения параллельной программы (например, распределение данных и вычислений) должна осуществляться динамически системой поддержки выполнения DVM-программ. Это позволяет обеспечить динамическую настройку DVM-программ при запуске (без перекомпиляции) на параметры приложения (количество и размер массивов данных) и конфигурацию параллельного компьютера (количество процессоров и их производительность). Тем самым программист получает возможность иметь один вариант программы для выполнения на последовательных ЭВМ,  параллельных ЭВМ различной конфигурации и неоднородных сетях ЭВМ. Кроме того, на основании информации о выполнении DVM-программы на однопроцессорной ЭВМ можно посредством моделирования работы системы поддержки предсказать характеристики выполнения этой программы на параллельной ЭВМ с заданными параметрами (производительность процессоров и характеристики коммуникационных каналов).

DVM-система состоит из следующих компонент:

·      Компиляторы с языков FORTRAN-DVM  и C-DVM.

·      Система поддержки выполнения параллельных программ;

·      Отладчик параллельных программ;

·      Анализатор производительности;

·      Предсказатель производительности.

3. Языки программирования Fortran-DVM и C-DVM

3.1. Директивы (спецификации) параллелизма

Программы на языках Fortran-DVM и C-DVM, помимо описания алгоритма обычными средствами языков Фортран 77 или Си, содержат директивы (спецификации) параллелизма. Директивы описываются на языке Fortran-DVM в виде спецкомментариев следующего вида:

            <начало-директивы> <директива>

<начало-директивы> :: CDVM$ | *DVM$ | !DVM$

На языке C-DVM директивы описывается в виде спецмакросов следующего вида

DVM (директива).

Директивы на двух языках отличаются только синтаксисом. Семантика директив практически одинакова. Эти директивы "невидимы" для стандартных компиляторов, поэтому DVM–программа без изменений может выполняться как в параллельном, так и в последовательном режимах.

При распараллеливании программы пользователь должен выполнить следующие работы:

а) Выявить параллелизм на уровне задач и описать одномерные массивы задач.

б) Определить распределенные массивы и параллельные циклы.

в) Описать согласованное распределение массивов и вычислений (задач, витков параллельных циклов). Данные и вычисления, не специфицированные пользователем, автоматически размножаются по всем процессорам.

г) Описать общие данные, т.е. определить межпроцессорные зависимости по данным по распределенным измерениям массивов.

д) Отметить точки (операторы) программы, в которых используются новые значения общих данных.

Теоретически распараллеливание программы в модели DVM можно рассматривать как отображения индексных (дискретных)  пространств. В модели DVM определены следующие базовые индексные пространства: массивы задач, массивы данных, циклы и массив (решетка) виртуальных процессоров. Общая схема отображений приведена на рис.2. В результате отображений для каждого виртуального процессора определяется подмножество данных и подмножество вычислений (операторов). Согласование этих подмножеств управляется правилом собственных вычислений: данные всегда вычисляются на том процессоре, куда они отображены. С помощью перераспределения данных пользователь может варьировать загрузку процессоров. 

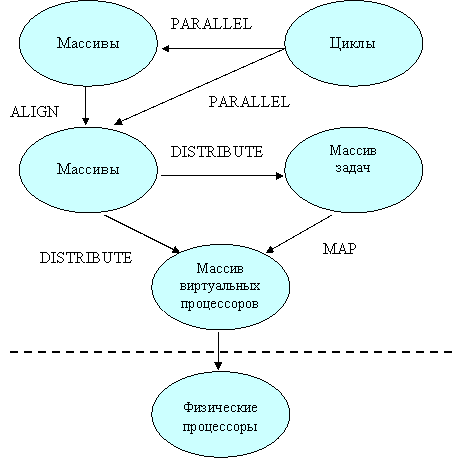
Рисунок 2.  Отображение последовательной программы.

3.2. Параллелизм задач

Параллелизм задач в модели DVM - это независимое по данным выполнение процедур и крупных блоков операторов. Если в программе существует такой уровень параллелизма, то пользователь должен описать одномерный массив задач с помощью директивы

CDVM$     TASK   TT(nt)

где nt – максимальное количество задач.

Каждую задачу необходимо отобразить на секцию массива виртуальных процессоров с помощью директивы

CDVM$     MAP  TT(i)  ONTO  P(n_i¹ : n _i², m _i¹ : m _i² )

где TT(i) - i-ая задача массива задач TT,

P – двумерный массив виртуальных процессоров.

Вычисления (блок операторов) отображаются на задачу с помощью директивы

CDVM$     ON  TT(i)

Отображение данных на задачу (см. п.3.3).

 

3.3. Отображение данных

Отображение данных осуществляется директивами DISTRIBUTE и ALIGN. Рассмотрим отображение одномерного массива (одного измерения).

CDVM$     DISTRIBUTE  AR (<формат>) [ONTO  T(n)]

<формат> = BLOCK – отображение равными блоками,

                 WGT_BLOCK(WB,NWB) – отображение взвешенными (неравными) блоками

                 * - отображение целым измерением

Пусть при запуске программы задана линейка виртуальных процессоров P(NP).

При отображении равными блоками индексное пространство измерения разделяется на NP блоков (отрезков) и i–ый блок отображается на виртуальный процессор P(i).

При отображении взвешенными блоками задается вектор весов WB размера NWB для каждой точки (или группы соседних точек) индексного пространства измерения. Измерение массива разделяется на NP блоков так, чтобы минимизировать отклонение веса каждого блока (суммы весов точек блока) от среднего  значения. Такое отображение позволяет сбалансировать загрузку процессоров.

Отображение целым измерением означает, что измерение не будет разделяться между процессорами и будет целиком распределено на каждый процессор (локальное, нераспределенное измерение).

Если присутствует опция ONTO T(n), то массив отображается на n‑ую задачу массива задач T, а точнее на ту часть линейки процессоров P(NP), на которую отображена  n‑ая задача.

Отображение многомерного массива осуществляется посредством задания отображения каждого его измерения. При этом  количество распределенных измерений массива не может превышать количество измерений решетки процессоров.

Очень часто требуется отобразить несколько массивов согласованно. Согласованное  отображение нескольких массивов требуется и для того, чтобы уменьшить количество  общих данных (данных, вычисляемых на одних процессорах и используемых на других), доступ к которым требует существенных накладных расходов.

Для организации согласованного  отображения нескольких массивов используется  механизм выравнивания одного массива на другой с помощью директивы ALIGN.

Рассмотрим следующий фрагмент программы

                 real  A(N), B(N)

CDVM$   DISTRIBUTE  A (BLOCK)

CDVM$   DISTRIBUTE  B (BLOCK)

                        .   .   .

CDVM$   PARALLEL  ( i )  ON  B( i )

                 do  i = n1,n2

                        B( i ) = A( f( i ))

                 enddo

Пусть OWN(B(i))  обозначает виртуальный процессор, на который распределен элемент B(i). Виток цикла с индексом i будет выполняться на процессоре OWN(B(i)). Если элемент A(f(i)) будет распределен на процессор OWN(B(i)), то для каждого витка цикла все данные будут распределены на одном процессоре. Чтобы обеспечить такую локализацию данных, необходимо вместо директивы

CDVM$         DISTRIBUTE  B (BLOCK)

применить директиву выравнивания индексных пространств массивов

CDVM$         ALIGN  B( i )  WITH  A( f( i ))

Директива устанавливает соответствие между элементами B(i) и A(f(i)). Это означает, что элемент B(i) будет распределен на процессор OWN(A(f(i))).

Замечание. При выполнении программы можно динамически изменять распределение данных с помощью директив REDISTRIBUTE и REALIGN. Однако надо понимать, что такое перераспределение  может потребовать  значительных затрат времени.

3.4. Параллелизм циклов

Директива PARALLEL встроена в язык Фортран в виде спецкомментария

CDVM$   PARALLEL (i₁,…,i_m)  ON  A(L₁,…,L_n)

где

L_k = a_k*i_j + b_k – линейная функция от индекса j–ого цикла (из m-мерного тесно-гнездового цикла), 0 < k < (n+1), 0 < j < (m+1)

A – идентификатор массива данных или массива задач.

Директива устанавливает соответствие между витком многомерного цикла с индексами (i₁,…,i_m) и элементом A(L₁,…,L_n). Это означает, что виток цикла будет выполняться на том процессоре, куда будет отображен элемент массива A(L₁,…,L_n).

3.5. Спецификация общих данных

Общие  данные,  т.е. данные, вычисляемые на одних процессорах и используемые на других процессорах, можно разбить на две основные категории.

Во-первых, общие данные, возникающие при  выполнении на разных процессорах разных параллельных конструкций программы. Такие общие данные отражают зависимость по данным между этими параллельными конструкциями, для учета которой необходимо организовать пересылку общих данных после выполнения первой конструкции и до начала выполнения второй. Примерами служат "Соседние" общие данные и REMOTE-данные. 

Во-вторых, общие данные, возникающие при  выполнении на разных процессорах одной параллельной конструкции. Они отражают имеющуюся в этой конструкции зависимость по данным. В общем случае такая конструкция не может выполняться на распределенных системах параллельно с приемлемой эффективностью. Но в определенных случаях (довольно часто встречающихся) можно организовать эффективное параллельное выполнение этой конструкции. Примерами служат редукционные данные и ACROSS-данные.

"Соседние" общие данные

Рассмотрим следующий фрагмент программы

CDVM$   PARALLEL  ( i )  ON  B( i ), SHADOW_RENEW (A(d1:d2))

                 do  i = d1+1, N-d2

                        B( i ) = A( i-d1 ) + A( i+d2 )

                 enddo

Требуемые каждому процессору общие данные размещены на соседних виртуальных процессорах. Спецификация SHADOW_RENEW указывает, что в данном цикле используются новые значения общих данных из массива A, d1  указывает размер требуемых  данных с левого соседа, а d2 – с правого. Для доступа к удаленным данным используются “теневые” грани. Теневая грань представляет собой буфер, который является непрерывным продолжением локальной секции массива в памяти процессора. Перед выполнением цикла требуемые удаленные данные пересылаются с соседних процессоров   в теневые грани массива А на каждом процессоре. Доступ к этим данным при выполнении цикла производится обычным образом (через ссылки на массив A).

Существует асинхронная форма спецификации, которая позволяет совместить пересылку данных в теневые грани с вычислениями.

REMOTE-данные

     Иногда доступ к удаленным данным требует заведения специальных буферов и соответствующей замены “удаленных” ссылок – ссылок на массив, через которые происходят обращения к удаленным элементам массива.

Рассмотрим следующий фрагмент программы

                   DIMENSION  A(100,100),  B(100,100)

     CDVM$ DISTRIBUTE  A (*,BLOCK)

     CDVM$ ALIGN  B( I, J )  WITH  A( I, J )

                   .   .    .

     CDVM$ REMOTE_ACCESS  ( A(50,50) )

     С            замена ссылки A(50,50) ссылкой на буфер и

     С            рассылка значения A(50,50) по всем процессорам

     1            X = A(50,50)

                   .   .   .

     CDVM$ REMOTE_ACCESS  ( B(100,100) )

     С            пересылка значения В(100,100) в буфер процессора own(A(1,1)

     2            A(1,1) = B(100,100)

                   .   .   .

     CDVM$ PARALLEL  (I,J)  ON  A(I,J) ,  REMOTE_ACCESS  ( B(I,N) )

     С            рассылка значений B(I,N) по процессорам own(A(I,J))

     3            DO 10  I = 1, 100

                   DO 10  J = 1, 100

     10          A(I,J) = B(I,J) + B(I,N)

 

Первые две директивы REMOTE_ACCESS специфицируют удаленные ссылки для отдельных операторов. REMOTE_ACCESS в параллельном цикле специфицирует удаленные данные (элементы N-го столбца матрицы B) для  всех процессоров, на которых выполняется цикл (при этом на каждый процессор будет переслана только необходимая ему часть столбца матрицы B).

Редукционные данные

Рассмотрим следующий фрагмент программы

CDVM$   PARALLEL  ( i )  ON  B( i ),  REDUCTION ( SUM(s))

                 do  i = 1, N

                        s= s+B( i )

                 enddo

Вообще говоря, имеющаяся зависимость по данным (переменная s) требует последовательного выполнения витков цикла с передачей значения переменной s от каждого отработавшего процессора к следующему. Однако если пренебречь влиянием отсутствия ассоциативности машинных операций сложения, то можно эффективно распараллелить такой цикл. Для этого на каждом процессоре заводятся копии переменной s,  в которых при параллельном выполнении цикла будут посчитаны частичные суммы. После выполнения цикла необходимо посчитать глобальную сумму посредством суммирования всех частичных сумм.

Аналогично можно поступить для распараллеливания циклов, в которых вычисляется максимальное или минимальное значение элементов массива. Такие общие данные называются редукционными. При их спецификации необходимо указать ту редукционную операцию, которую требуется выполнить после цикла для объединения частичных результатов, посчитанных на каждом процессоре.

ACROSS-данные

Рассмотрим фрагмент программы

CDVM$   PARALLEL  ( i )  ON  B( i ),  ACROSS (B(d1:d2))

                 do  i = d1+1, N-d2

                        B( i ) = B( i-d1 ) + B( i+d2 )

                 enddo

ACROSS-данные (элементы массива B) также являются соседними общими данными. Но они используются и обновляются в одном и том же цикле (в цикле имеется зависимость по этим данным). Параметры d1 и d2  указывают размеры общих данных на соседних процессорах слева и справа, соответственно. Такая  зависимость по данным в общем случае требует последовательного выполнения витков цикла с передачей значений обновленных общих данных от каждого отработавшего процессора к следующему. Однако во многих случаях, например, когда двумерный цикл распределен по одному измерению на линейку процессоров, можно эффективно распараллелить такой цикл, если организовать его конвейерное выполнение. Идея конвейерного выполнения заключается в том, что первый процессор выполняет часть “своих” витков цикла и передает следующему процессору соответствующую порцию обновленных общих данных. После получения этих данных второй процессор начинает выполнять “свои” витки цикла параллельно с выполнением первым процессором второй порции витков, и т.д. Оптимальный размер порции витков зависит от количества витков цикла, времени выполнения каждого витка, числа процессоров, а также латентности и пропускной способности коммуникационной среды. Система поддержки DVM‑программ обеспечивает вычисление оптимальной порции витков и соответствующее дробление одного или нескольких измерений цикла, а также передачу обновленных общих данных между процессорами.

4. Пример  параллельной программы на языке Fortran-DVM. Алгоритм Якоби.

       PROGRAM    JAC_DVM 

       PARAMETER    (L=8,  ITMAX=20) 

       REAL     A(L,L), B(L,L) 

CDVM$  DISTRIBUT  A (BLOCK,BLOCK)  

CDVM$  ALIGN  B(I,J)  WITH  A(I,J)

C      массивы A и B распределяются блоками 

       DO IT  =  1,  ITMAX 

CDVM$  PARALLEL  (J,I)   ON  A(I,  J)          

         DO  J  =  2, L-1         

           DO  I  =  2, L-1                    

             A(I, J)  =  B(I, J)         

           ENDDO         

         ENDDO 

CDVM$  PARALLEL  (J,I) ON B(I,J),SHADOW_RENEW (A)

C    двумерный параллельный цикл, итерация (i,j) выполняется,

C    на том процессоре, где размещен элемент B(j,i) 

C    копирование теневых элементов массива A

C    с соседних процессоров перед выполнением цикла

         DO  J = 2,  L-1         

           DO  I = 2,  L-1              

             B(I, J) =  (A( I-1, J ) + A( I, J-1 ) + 

     *                   A( I+1, J ) + A( I, J+1 )) / 4         

           ENDDO        

         ENDDO         

       ENDDO

END

 

Директива DISTRIBUTE описывает следующее распределение массива А. Массив А распределяется на двумерную решетку процессоров. Количество форматов BLOCK определяет количество измерений решетки виртуальных процессоров. Первое измерение массива А распределяется равными блоками по первому измерению решетки процессоров, второе измерение – по второму измерению решетки. При запуске программы на выполнение может быть задана любая двумерная решетка процессоров.

Директива ALIGN определяет распределение массива В, согласованное с распределением массива А: элемент B(I,J) будет распределен на тот же процессор, где размещен элемент A(I,J).

Оба цикла удовлетворяют требованиям параллельного цикла модели DVM. Обе директивы PARALLEL описывают распределение витков цикла, согласованное с распределением массивов: А и В: виток цикла с индексами (I,J)  будет выполняться на том же процессоре, где размещены элементы A(I,J) и B(I,J).

Анализ оператора присваивания первого цикла показывает, что левая и правая часть оператора присваивания для каждого витка цикла распределены на том же процессоре, где выполняется виток цикла (следствие выполнения директив ALIGN и PARALLEL).

Анализ второго цикла показывает, что не для каждого витка цикла выполняется локализация данных (отсутствие общих данных). Это определяется сравнением индексных выражений по каждому распределенному измерению левой и правой частей оператора. Если индексные выражения не равны и отличаются на постоянную небольшую величину, то в данном цикле возникают общие данные типа SHADOW. Спецификацией  SHADOW_RENEW(А) пользователь указывает, что в данном цикле используются новые значения общих данных. Реализация спецификации в системе поддержки показана на рис.3.

Во-первых, при распределении массива на каждый процессор распределяется не только секция массива, но и так называемые области перекрытия или теневые грани ( на рис.3 они показаны темным цветом). Ширина теневых граней определяется разницей индексных выражений в левой и правой части операторов присваивания. Для данного примера ширина всех граней равна 1.

Во-вторых, перед параллельным циклом со спецификацией SHADOW_RENEW(А) система поддержки произведет массовый обмен данными между «соседними» процессорами решетки. Схема обмена для одного процессора показана на рис.3.

 

 

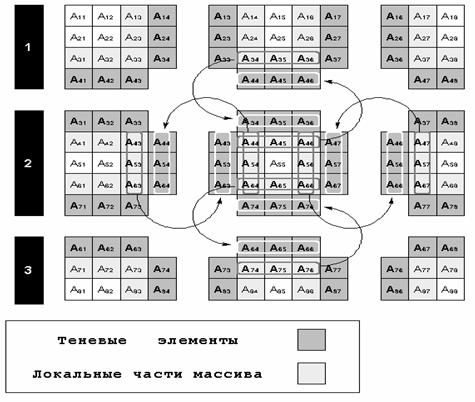
Рисунок 3.  Отображение массива A(8,8) на процессорную решетку 3*3

 

5. Компиляция и модель выполнения DVM-программ

Параллельная программа на исходном языке Fortran-DVM (или C-DVM) превращается в программу на  языке Фортран 77 (или Си), содержащую вызовы функций системы поддержки, и выполняющуюся в соответствии с моделью SPMD (одна программа – много данных) на каждом выделенном задаче процессоре.

Модель выполнения DVM-программы можно упрощенно описать следующим образом.

В момент запуска программы существует единственная её ветвь (поток управления), которая начинает свое выполнение с первого оператора программы сразу на всех процессорах виртуальной многопроцессорной системы.

Виртуальной многопроцессорной системой   называется та машина, которая предоставляется программе пользователя аппаратурой и базовым системным программным обеспечением. Для распределённой ЭВМ примером такой машины может служить MPI-машина. В этом случае, виртуальная многопроцессорная система - это группа MPI-процессов, которые создаются при запуске параллельной программы на выполнение. Число процессоров виртуальной многопроцессорной системы и её представление в виде многомерной решетки задаётся в командной строке при запуске программы.

Все объявленные в программе переменные (за исключением специально указанных "распределённых" массивов) размножаются по всем процессорам.

При входе в параллельную конструкцию (параллельный цикл или область параллельных задач) ветвь разбивается на некоторое количество параллельных ветвей, каждая из которых выполняется на выделенных ей процессорах.

 При выходе из параллельной конструкции все ветви сливаются в ту же самую ветвь, которая выполнялась до входа в параллельную конструкцию.

 

6. Эффективность выполнения DVM-программ

 

Эффективность выполнения программ всегда являлась очень важным фактором, определявшим в значительной степени успех и распространение языков программирования, предназначенных для создания вычислительных программ.

Для DVM-программ вопрос эффективности выполнения носит принципиальный характер, поскольку эти программы должны при запуске динамически (без перекомпиляции) настраиваться на количество и производительность выделенных для их выполнения процессоров. Для оценки эффективности выполнения DVM-программ были разработаны соответствующие версии тестов NPB 2.3 [7].

Эти тесты хорошо отражают характер вычислительных задач различных классов, за исключением задач с нерегулярными сетками. Ниже дается краткая характеристика тестов, и приводятся их размеры в строках для трех версий каждой программы – последовательной версии, MPI-версии и DVM-версии.

 

 

SEQ  – поcледовательная программа

MPI  – параллельная программа с использованием 77+MPI или Си+MPI (IS)

DVM – параллельная программа на языке Fortran-DVM или C-DVM (IS)

   Ниже  для каждого  теста приведены отношения времени выполнения его MPI-версии к времени выполнения  DVM-версии на ЭВМ МВС-1000М [8].

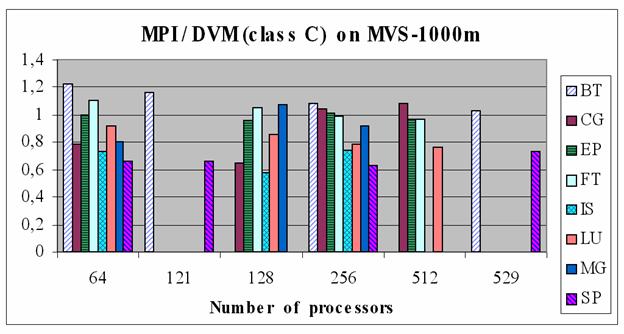
Замечание. В таблице отсутствуют результаты сравнения для тестов IS и MG на 512-ти процессорах, поскольку  не удалось пропустить MPI-версии этих тестов.

 

Конечно, сравнение на тестах NPB 2.3 не вполне правомерно – они написаны на очень высоком профессиональном уровне и являются объектом пристального внимания многих специалистов. При разработке реальных параллельных программ, как правило, достижение высокой эффективности требует многократных изменений программы для поиска наилучшей схемы ее распараллеливания. Успешность такого поиска определяется простотой модификации программы. Кроме того, прикладному программисту трудно реализовать многие часто используемые приемы распараллеливания так же эффективно, как они реализуются системами программирования. Поэтому на реальных программах MPI-подход, очень часто проигрывает по эффективности DVM-подходу.

 

7. Переносимость и повторное использование параллельных программ

В настоящее время, когда программист имеет возможность запускать свою программу на разных, порою географически удаленных параллельных системах,   важность переносимости программ (их способности выполняться на различных вычислительных системах с приемлемой эффективностью) трудно переоценить.

Создать для новых параллельных систем прикладное программное обеспечение, необходимое для решения важнейших научно-технических задач, вряд ли возможно без повторного использования уже созданных программ, без накопления и использования богатых библиотек параллельных программ.

Поэтому переносимость программ и их способность к повторному использованию должны рассматриваться как самые первостепенные показатели качества параллельных программ.

Огромная заслуга разработчиков MPI заключается в обеспечении переносимости параллельных программ на различные многопроцессорные ЭВМ с распределенной и общей памятью. Однако перенос MPI-программ на неоднородные (по производительности процессоров) кластеры и сети ЭВМ приведет к заметной потере их эффективности, поскольку прикладной программист фактически не имеет возможностей для   написания программ, способных настраиваться на  производительность разных процессоров.

Кроме того, при использовании MPI очень сложно разрабатывать программы, способные выполняться на различном числе процессоров с разными по объему данными. Многие программисты предпочитают иметь разные варианты программ для разных конфигураций данных и процессоров, а также иметь отдельный вариант программы для работы на однопроцессорной ЭВМ. В таких условиях использование чужой программы представляется гораздо менее вероятной, чем это было на традиционных ЭВМ. 

Но главные трудности связаны с отсутствием в языке программирования такого понятия, как распределенный массив. Вместо такого единого массива в программе используется на каждом процессоре свой локальный массив. Их соответствие исходному массиву, с которым программа имела бы дело при ее выполнении на одном процессоре, зафиксировано только в голове программиста и, возможно, в комментариях к программе.

Как уже говорилось выше, DVM-программы могут без каких-либо изменений компилироваться и выполняться на последовательных ЭВМ в среде компиляторов Фортран 77/90 или Си.

Переносимость DVM-программы на  произвольные кластеры или сети ЭВМ обеспечивается тем, что она  преобразуется в программу на  языке Фортран 77 (или Си), содержащую вызовы функций системы поддержки, которая для организации межпроцессорного взаимодействия использует библиотеку MPI. Такая программа может выполняться всюду, где есть MPI и компиляторы с языков Си и Фортран 77.

Кроме того, программы на языке Fortran-DVM могут автоматически конвертироваться в программы на языке HPF или HPF2. Планируется в дальнейшем обеспечить и автоматическое преобразование DVM-программ в OpenMP-программы.

Повторное использование DVM-программ существенно облегчается в силу следующих причин:

-         наглядность и явная спецификация параллельного выполнения DVM-программы;

-         гибкость настройки программы на входные параметры приложения (число массивов и их размеры) и количество выделенных процессоров;

-         гибкость настройки процедуры на фактические параметры – распределенные массивы.

8. Средства  отладки

Отладка параллельной программы является процессом более трудоемким, чем отладка последовательной программы. Причиной этого является не только сложность параллельной программы, но и ее недетерминированное поведение, серьезно затрудняющее и функциональную отладку (достижение правильности результатов), и отладку эффективности программы. Раньше с подобными трудностями сталкивались, в основном, разработчики операционных систем и систем реального времени, которые сами и создавали для себя специальные средства отладки. Развитые средства отладки могут существенно упростить разработку параллельных программ прикладными программистами. Поэтому отладке программ в DVM-системе уделено особое внимание.

Функциональная отладка DVM-программ [9] осуществляется поэтапно:

·         Сначала программа отлаживается на рабочей станции как обычная последовательная программа с использованием штатных средств отладки.

·         Затем на той же рабочей станции программа пропускается в специальном режиме проверки DVM-указаний, что позволяет выявить их правильность и полноту.

·         На следующем этапе программа может быть пропущена на параллельной машине (или рабочей станции, имитирующей параллельную машину) в режиме сравнения промежуточных результатов ее параллельного выполнения с эталонными результатами, полученными при ее последовательном выполнении.

Для отладки программы на реальной параллельной машине используются также средства накопления трассировки, позволяющие зафиксировать последовательность обращений к переменным и их значения, а также последовательность вызовов функций системы поддержки выполнения DVM-программ.

Для отладки эффективности DVM-программ используется  анализатор производительности,  который позволяет пользователю получить информацию об основных характеристиках эффективности выполнения его программы (или ее частей) на параллельной системе.

Для облегчения отладки эффективности можно использовать специальный инструмент – предсказатель производительности. Он позволяет на рабочей станции смоделировать выполнение DVM-программы на параллельной ЭВМ с заданными параметрами (топология коммуникационной сети, ее латентность и пропускная способность, а также производительность процессоров) и получить прогнозируемые характеристики эффективности ее выполнения.

9. Выводы

Перечислим основные достоинства DVM-системы:

·        высокоуровневая модель программирования, позволяющая описывать алгоритм в терминах массива целиком, а  не требовать от программиста манипулирования локальными частями массива, размер которых зависит от числа используемых процессоров;

·        возможность иметь один вариант программы для эффективного выполнения на последовательных ЭВМ и параллельных ЭВМ различной конфигурации и (и с различной производительностью процессоров);

·        высокоуровневые средства функциональной отладки, анализа и предсказания эффективности.

 

Система DVM может использоваться на рабочих станциях (SGI, HP, IBM, SUN)  и персональных ЭВМ с операционными системами UNIX и WINDOWS 95/98/2000/NT.

Система установлена на следующих параллельных ЭВМ и кластерах:

·        МВС-1000M (МСЦ)

·        МВС-1000/16 (ИПМ им. М.В.Келдыша РАН и ИММ УрО РАН)

·        МВС-1000/200 (ИПМ им. М.В.Келдыша РАН)

·        Вычислительные кластеры SCI и SKY  (НИВЦ МГУ)

·        Вычислительный кластер NCI  (г.Пекин)

·        Parsytec CC  (ИММ РАН)

·        Convex SPP 1600 (ИПМ им. М.В.Келдыша РАН)

·        Вычислительный кластер ННГУ (г.Н.Новгород)

Система (в виде исходных текстов и  библиотек выполняемых программ) доступна через Интернет (http://www.keldysh.ru/dvm/). Вместе с системой поставляется набор демонстрационных DVM-программ, а также  документация пользователя и разработчика

 

Литература

1.    High Performance Fortran Forum. High Performance Fortran Language Specification. Version 1.0, May 1993.

2.    PCF Fortran. Version 3.1. Aug.1, 1990.

3.    OpenMP Consortium: OpenMP Fortran Application Program Interface, Version 1.0, October 1997. http://www.openmp.org/

4.    Konovalov N.A., Krukov V.A., Mihailov S.N. and Pogrebtsov A.A. Fortran DVM - a Language for Portable Parallel Program Development. Proceedings of Software For Multiprocessors & Supercomputers: Theory, Practice, Experience. Institute for System Programming, RAS, Moscow, 1994.

5.    Коновалов Н.А., Крюков В.А., Погребцов А.А., Сазанов Ю.Л. С-DVM - язык разработки мобильных параллельных программ // Программирование. 1999. №1.

6.    DVM-система. http://www.keldysh.ru/dvm/

7.    Bailey D., Harris T., Saphir W., Van der Wijngaart, Woo A., Yarrow M.The NAS Parallel Benchmarks 2.0. NAS Technical Report NAS-95-020, NASA Ames Research Center, Moffett Field, CA, 1995. http://science.nas.nasa.gov/Software/NPB.

8.    Елизаров Г.С., Забродин А.В., Левин В.К., Каратанов В.В.,  Корнеев В.В., Савин Г.И., Шабанов Б.М. Структура многопроцессорной вычислительной системы МВС-1000М. Труды Всероссийской научной конференции "Высокопроизводительные вычисления и их приложения", г.Черноголовка, 30 октября - 2 ноября 2000 г., Изд-во Московского университета, 2000.

9.    В.А.Крюков, Р.В.Удовиченко, “Отладка DVM-программ”, Программирование  2001, № 3, стр. 19-29