О семантике Дейталога

Введение.

В 70-е годы логическое программирование и базы данных развивались одновременно. Пролог – самый популярный язык ПРОграммирования в ЛОГике – появился как результат упрощения более общих методов доказательства теорем для достижения возможности эффективного программирования.  Аналогично реляционная модель данных возникла в результате упрощения сложных иерархической и сетевой моделей для обеспечения возможности непроцедурного манипулирования множественными данными. На протяжении 70-х и в начале 80-х годов Пролог и реляционные базы данных получили широкое распространение не только в академической или научной среде, но и в деловом мире.

Интенсивные исследования взаимосвязи логического программирования и реляционных баз данных проводились с конца 70-х годов главным образом с теоретической точки зрения. Успеху интеграции способствовало то обстоятельство, что Пролог был выбран в качестве парадигмы языка программирования в японском проекте ЭВМ 5-го поколения. Целью этого проекта является разработка «ЭВМ следующего поколения», ориентированных на применение в области искусственного интеллекта и, следовательно, способных выполнять исключительно большое число логических выводов в единицу времени. Проект также предусматривал использование реляционной модели данных для хранения больших совокупностей данных.

Поэтому были проведены исследования в пограничной области между логическим программированием и реляционными базами данных.

Логическое программирование обладает большей выразительной способностью задания запросов и ограничений в сравнении с языками определения данных и манипулирования данными систем баз данных. Более того, представление запросов и ограничений возможно при этом однородном формализме, и их проверка требует одних и тех же механизмов вывода, что позволяет вести более сложные рассуждения о содержимом базы данных. Вместе с тем системы логического программирования не обеспечивают технологии управления большими, надежными, долговременно хранимыми совокупностями данных с коллективным доступом.

Естественное расширение логического программирования и управления базами данных заключается в построении новых классов систем, расположенных на пересечении этих двух областей. Такие системы основаны на использовании логического программирования в качестве языка запросов и соединяют формулирование запросов и ограничений в стиле логического программирования с технологией баз данных для эффективного и надежного запоминания данных в массовой памяти.

Логическое программирование как язык запросов

Дадим неформальное представление о том, как логическое программирование может использоваться в качестве языка запросов. Для простоты восприятия в Таблице 1 представлены соответствия понятий логического программирования и баз данных.

Рассмотрим реляционную базу данных с двумя отношениями PARENT(PARENT, CHILD) и PERSON(name, age, sex). Кортеж отношения PARENT (родитель) содержит пары субъектов, находящихся в отношении родитель – ребенок, кортежи отношения PERSON (личность) содержат триплеты, первым, вторым и третьим элементом которых соответственно являются имя, возраст и пол личности.

Содержимое базы данных представлено на Рисунке 1.

 

 

Понятия баз данных

Понятия логического программирования

Отношение

Предикат

Атрибут

Аргумент предиката

Кортеж

Базовый дизъюнкт (факт)

Представление

Правило

Запрос

Цель

Ограничение

Цель (логическое значение)

Таблица 1

 

PARENT

PARENT

CHILD

john

jeff

jeff

margaret

margaret

annie

john

anthony

Рисунок 1

Представим простые запросы к базе данных на языке логического программирования. При использовании Пролога предполагается, что читатель имеет некоторое представление о нем. В примере используются два специальных предиката базы данных PARENT и PERSON в предположении, что базовые дизъюнкты (факты) для этих предикатов хранятся в базе данных. Например, кортеж <john, jeff> отношения базы данных PARENT соответствует базовому дизъюнкту parent(john, jeff).

Запрос «Кто дети Джона?» выражается с помощью следующей цели Пролога:

? – parent (john, X).

Ожидаемый в результате применения этого запроса к базе данных ответ:

X = {jeff, anthony}.

Ответ формируется следующим образом. Предполагается, что факты заданы в основной памяти в указанном выше порядке. При реализации цели переменная X вначале устанавливается равной jeff; если пользователь требует новых ответов, переменная X устанавливается равной anthony; если пользователь снова требует новых ответов, поиск терпит неудачу и интерпретатор отвечает no. Заметим, что Пролог возвращает результат по одному кортежу, а не как множество результирующих кортежей.

Можно представить запросы, в которых все аргументы являются константами. Например,

? – parent (john, jeff).

В этом случае ожидается положительный ответ, если кортеж <john, jeff> принадлежит базе данных, и отрицательный результат в противном случае. В нашем примере система Пролог продуцирует ответ yes.

Правила можно использовать для построения интенсиональной базы данных (ИБД) из экстенсиональной базы данных (ЭБД). ЭБД – это просто реляционная база данных. В нашем примере она включает отношения PARENT и PERSON. ИБД строится из ЭБД с помощью правил, определяющих ее содержимое, а не с помощью явного хранения ее кортежей.

Пример:

father(X, Y) :- person(X, _, male), parent(X, Y).

mother(X, Y) :- person(X, _, female), parent(X, Y).

Более сложные отношения ИБД конструируются с помощью рекурсивных правил, т. е. правил, в которых предикат головы включается в тело правила. Пример – отношение ANCESTOR  включает в качестве кортежей все пары предок – потомок, начиная от родителей:

ancestor(X, Y) :- parent(X, Y).

ancestor(X, Y) :- parent(X, Z), ancestor(Z, Y).

Пример проверки ограничения (никто не рождает сам себя или каждая личность имеет единственную мать).

incorrectdb :- parent(X, X).

incorrectdb :- mother(X, Z), mother(Y, Z), not(X = Y).

Единообразие позволяет в ограничениях  использовать предикаты ИБД, и не только проверять непротиворечивость баз данных, но и выяснять (а потом и устранять) источники противоречий. Мы не будем надолго останавливаться на этом.

Пролог и Дейталог

Выше мы показали, как интерпретатор Пролога оперирует базой фактов, и продемонстрировали, что Пролог может работать как мощный язык баз данных. Выбор Пролога для иллюстрации использования логического программирования в качестве языка баз данных практически не вызывает сомнений, поскольку Пролог является наиболее популярным языком логического программирования. Однако использование  Пролога в данном контексте иллюстрирует ряд недостатков, которые частично обнаружились в нашем примере. К ним можно отнести следующее:

1.      Покортежная обработка. Хотя мы ожидали, что результатом запросов к базе данных должно быть множество кортежей, Пролог возвращает отдельные кортежи по одному.

2.      Процедурность и чувствительность к порядку. Обработка в Прологе зависит от порядка правил или фактов в базе данных и  от порядка предикатов в теле правила. В действительности программист на Прологе использует чувствительность к порядку для построения эффективных программ, жертвуя, таким образом, декларативной природой логического программирования в пользу процедурности. Напротив, языки баз данных (такие, как SQL или реляционная алгебра) являются непроцедурными: выполнение запросов к базе данных не зависит от порядка поисковых предикатов или кортежей базы данных.

3.      Специальные предикаты. Программисты на Прологе управляют выполнением программ с помощью специальных предикатов (используемых, например, для ввода-вывода, отладки или для воздействия на бэктрекинг). В этом заключается другая важная причина потери декларативной природы языка, не имеющей аналогов в языках программирования.

4.      Функциональные символы. Пролог содержит функциональные символы, используемые обычно для построения рекурсивных функций и сложных структур данных; эти функции не требуются для манипулирования плоской реляционной базой данных, хотя они могли бы оказаться полезными для оперирования сложными объектами в базах данных. Однако эти вопросы мы не будем рассматривать.

Альтернативой Прологу как языку баз данных и логического программирования оказался язык Дейталог, который сконструирован для использования в качестве языка баз данных. Он является непроцедурным, множественным, нечувствительным к порядку, не имеющим специальных предикатов и функциональных символов. Таким образом, в Дейталоге устранены четыре указанных выше недостатка Пролога.

Синтаксически Дейталог напоминает чистый Пролог. Все прологовские правила, приведенные выше для представления запросов и ограничений, являются также правильными запросами Дейталога. Их выполнение приводит к образованию множества кортежей; например, после реализации цели

? – parent(john, X).

Мы получим X = {jeff, anthony}.

В качестве примера различной чувствительности Пролога и Дейталога к порядку рассмотрим следующие две программы:

Программа Предок1:

ancestor(X, Y) :- parent(X, Y).

ancestor(X, Y) :- parent(X, Z), ancestor(Z, Y).

Программа Предок2:

ancestor(X, Y) :- ancestor(Z, Y), parent(X, Z).

ancestor(X, Y) :- parent(X, Y).

Входная цель:

? – ancestor(X, Y).

Обе программы Предок1 и Предок2 являются синтаксически правильными как на Дейталоге, так и на Прологе. Дейталог нечувствителен ни к порядку правил, ни к порядку предикатов в правилах; поэтому он производит правильный ответ в обоих вариантах. Наоборот, интерпретатор Пролога демонстрирует ожидаемое поведение в версии Предок1, но он зацикливается в версии Предок2. В действительности программист на Прологе должен следить за тем, чтобы программа не зацикливалась, тогда как программист на Дейталоге может не заботиться об этом.

Эволюция от  Пролога к Дейталогу состоит в движении от процедурного, ориентированного  на обработку записей языка к непроцедурному языку, ориентированному на обработку множеств, и что такой процесс характерен для эволюции языков баз данных от иерархических и сетевых баз данных к реляционным базам данных. Хотя Дейталог является декларативным языком и его определение не зависит от какой-либо стратегии поиска, цели Дейталога обычно вычисляются с помощью стратегии поиска «сначала вширь», которая порождает множество всех ответов, а не с помощью стратегии поиска Пролога «вглубь», порождающей ответы в рамках покортежного подхода. Это согласуется с множественным подходом реляционных языков запросов. Более того,  в Дейталоге программист не задает процедуры доступа к данным, что является прерогативой системы; это снова хорошо согласуется с реляционными языками запросов, которые являются непроцедурными.

Однако эти особенности ограничивают мощность Дейталога как универсального языка программирования. В действительности Дейталог образуется в результате исключения некоторых функций из Пролога (удаляемых не навсегда) и в добавлении к нему средств, относящихся к классическим языкам баз данных.

Поэтому Дейталог рассматривается главным образом как хорошая абстракция, иллюстрирующая использование логического программирования как языка баз данных, а не универсального языка. Можно, однако, ожидать, что Дейталог будет эволюционировать в направлении приобретения некоторых других средств и превратится в универсальный язык в ближайшем будущем.

 

Семантика Дейталога

Попробуем дать ответ на вопрос: «Что вычисляет программа на Дейталоге?». Мы считаем программу на Дейталоге запросом, оперирующим над экстенсиональной базой данных и вычисляющим некоторый результат. Результат программы Дейталога P, примененной к EDB E, состоит из всех основных фактов, которые являются логическим следствием множества дизъюнктов и предикатные символы которых лежат в IPred. .

Мы не будем давать формальное определение логического следствия, но осознать понятие можно из связи логического следствия (обозначается как S |= G) и импликации: если из A логически следует B, то A имплицирует B (теорема). Следовательно, смысл (или семантику) программы Дейталога можно описать с помощью отображения, связывающего множество интенсиональных фактов со всеми возможными экстенсиональными множествами.

Программа Дейталога действительно подобна тому, что принято называть запросом, так как каждому экземпляру базы данных ставит в соответствие результат. Единственным существенным отличием является то, что результат программы Дейталога может содержать факты для нескольких интенсиональных предикатов, в то время как результат запроса обычно состоит из одного-единственного отношения. Тем не менее, если в дополнение к программе Дейталога мы задаем цель, результат состоит из основных фактов только для одного предиката. Однако наше описание семантики Дейталога не содержит намека на то, как следует вычислять запрос логической программы.

Вывод фактов

Попробуем ответить на вопрос, как же вычислять программу Дейталога, получать новые факты. Рассмотрим правило Дейталога R вида L0 :- L1, …, Ln и список основных фактов F1, …., Fn. Если существует подстановка  такая, что для всех 1 <= i <=n  , то из правила R и из фактов F1, …., Fn можно вывести за один шаг факт . Выведенный факт может быть новым фактом или уже известным. Это правило называется элементарной продукцией (ЭП).

Пример. Рассмотрим правило Дейталога R: p(X, Z) :- p(X, Y), p(Y, Z) и основные факты {p(a, b)} и {p(b, c)}. Тогда с помощью ЭП можно вывести за один шаг факт {p(a, c)}, используя подстановку Это - новый факт. Теперь рассмотрим правило Дейталога R`: p(X, Y) :- p(Y, X) и факт {p(a, a)}. Очевидно, применяя ЭП, нельзя вывести ничего нового, кроме {p(a, a)}, т. е. самого факта.

Для вычисления множества всех фактов, которые могут быть выведены за один шаг с помощью ЭП, требуется перебрать все упорядоченные множества всех фактов базы данных и проверить, применима ли ЭП. Если она применима, то новый факт нужно присоединить к результату.  Эту процедуру назовем infer1.

Определим, наконец, понятие выводимых основных фактов. Пусть S – множество дизъюнктов Дейталога. При неформальной трактовке основной факт G может быть выведен из S, что обозначается S |- G, тогда и только тогда, когда либо , либо G можно получить, применяя правило ЭП конечное число раз.

·        S |- G, если .

·        S |- G, если правило и существуют основные факты F1, …., Fn такие, что  S |- Fi и G может быть выведено за один шаг применением ЭП к R и F1, …., Fn.

·        Во всех других случаях S |- G не выполняется.

Последовательность применений ЭП, которая используется для вывода основного факта G из S, называется доказательством G. Любое доказательство может быть представлено с помощью дерева доказательства с различными уровнями. Ниже располагаются дизъюнкты, выведенные раньше. В самом низу находятся исходные дизъюнкты.

Пример. Рассмотрим множество S дизъюнктов Дейталога, включающее правила R1: p(X, Z) :- p(X, Y), p(Y, Z) и R2: p(X, Y) :- p(Y, X) и основной факт {p(a, b)}.

Дерево доказательства имеет глубину 2 и включает 2 ЭП:

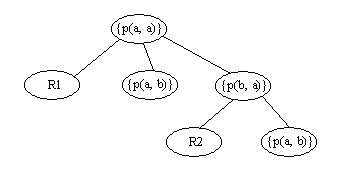
Рисунок 2

Оказывается, что правило ЭП является полным, т. е. оно эквивалентно логическому следствию. Мы не будем доказывать этого утверждения, хотя оно строго доказуемо.

Утверждение 1. Выводимость эквивалентна логическому следствию. S |-GS |=G.

Итерация наименьшей неподвижной точки

Обратимся к теории неподвижной точки. Эта теория первоначально создавалась в теории рекурсии – подраздела математической  логики – как средство объяснения рекурсивных функций. Позднее она была использована в ряде  других областей математики – таких, как алгебра и функциональный анализ. В информатике эта теория может с успехом применяться, когда требуется формальное описание семантики рекурсивных программ или систем.

Одной из главных особенностей языков логического программирования является их способность изображать рекурсию. Следовательно, теория неподвижной точки пригодна для определения семантики этих языков. Этот вид семантики, называемой обычно семантикой неподвижной точки, имеет ряд достоинств, таких, как непроцедурность, совмещаемая со способностью точного изображения вычислений.

Основным результатом теории неподвижной точки является теорема о неподвижной точке.

Теорема (о неподвижной точке). Пусть T – монотонное преобразование на полной решетке. Тогда Т имеет наименьшую неподвижную точку.

Нам важно, во-первых, что полная решетка -  это частично упорядоченное множество, т. е. на нем введено бинарное отношение, являющееся частичным порядком. Во-вторых, Т – монотонное преобразование. Постараемся применить эту теорему, чтобы установить семантику неподвижной точки программ на Дейталоге.

Будем рассматривать решетку V = , где F – множество подмножеств множества всевозможных фактов, а «» - обыкновенное включение множеств. Возьмем infer1. Таким образом, TS(W) – это очередной шаг применения всех правил программы Дейталога к W с присоединением всех накопленных старых. Очевидно, что TS – монотонное преобразование, так как монотонно infer1.

Применение теоремы о неподвижной точке к преобразованию T дает нам две вещи. Во-первых, с ее помощью и с помощью утверждения 1 (об эквивалентности логического следствия и выводимости фактов) мы получаем другое определение семантики  программы Дейталога P. Для конечной  . Пересечение c означает всего лишь, что нас интересуют только интенсиональные факты.

Во-вторых, мы получаем способ вычисления неподвижной точки преобразования TS.

Пользуясь последним высказанным утверждением, можно составить алгоритм на некотором метаязыке вычисления результата программы Дейталога:

АЛГОРИТМ LFP(S)

INPUT: конечное множество S дизъюнктов Дейталога

OUTPUT: результат программы Дейталога, т.е. множество всех основных фактов, являющихся следствиями S.

BEGIN

old := ;

new := FACTS(S);

WHILE new <> old DO

BEGIN

old := new;

new := old FACTS(S)  infer1(RULES(S)  old)

END;

RETURN result

END.

Пример. Рассмотрим множество S дизъюнктов Дейталога, включающее правила R1: anc(X, Y) :- anc(Z, Y), par(X, Z) и R2: anc(X, Y) :- par(X, Y) и основные факты {p(a, b)}, {p(b, c)}, {p(b, d)}, {p(c, e)}.

Покажем, как работает LFP, перечислением значений, которые принимает переменная new при каждой итерации. Пусть newi обозначает значение new после i-го повторения цикла.

new0 =  FACTS(S) = {{p(a, b)}, {p(b, c)}, {p(b, d)}, {p(c, e)}};

new1 = new0  FACTS(S)  infer1(RULES(S)) = new0  {{a(a, b)}, {a(b, c)}, {p(b, d)}, {p(c, e)}};

 new2 = new1  FACTS(S)  infer1 (RULES(S)  new1) = new1  {{a(a, c)}, {p(a, d)}, {a(b, e)}};

new3 = new2  FACTS(S)  infer1 (RULES(S)  new2) = new2  {{a(a, e)}};

new4 = new3.

Вычисление, реализуемое с помощью алгоритма LFP, называется восходящим вычислением, поскольку алгоритм начинается с рассмотрения основных фактов S, которые составляют «нижнюю» часть деревьев доказательства, и осуществляет движение «вверх», продуцируя вначале все факты, которые могут быть вычислены за один шаг из самых нижних дизъюнктов. Затем все факты, которые могут быть вычислены за один шаг из самых нижних дизъюнктов или из фактов, которые были выведены за один шаг и т. д. После i-го повторения цикла будут накоплены все основные факты, для которых существует дерево доказательства с числом уровней i или меньше.

Один шаг ЭП также называется прямым выводом, потому  что если правила Дейталога представляются как импликации, они обрабатываются в «прямом» направлении в смысле знака импликации.

Существует также совершенно иная альтернатива восходящему (прямому выводу) вычислению программ на Дейталоге. Показано, как правила Дейталога могут обрабатываться в обратном направлении (начиная с целевого дизъюнкта) путем построения дерева доказательства нисходящим образом. Этот метод  называется также обратным выводом. Показано также, как известный метод резолюции можно использовать для ответа на запросы Дейталога.

Выразительная мощность Дейталога

Нерекурсивный Дейталог в точности эквивалентен RA+. Каждое правило Дейталога можно транслировать в уравнение RA+ и наоборот. RA+ (положительная реляционная алгебра) – это реляционная алгебра без операции разность). В RA нас интересуют только базовые операции - выборка, проекция, декартово произведение, объединение и разность. Это означает, что Дейталог по меньшей мере настолько же выразителен, как и RA+. Таким образом, полный Дейталог строго более выразителен, чем RA+, поскольку на Дейталоге можно выразить невыразимые в RA+ рекурсивные запросы. Например, отношение ANC можно выразить только с помощью рекурсивных правил или рекурсивных уравнений RA+. Это справедливо для большинства рекурсивных программ Дейталога.

С другой стороны, существуют выражения полной реляционной алгебры, которые нельзя выразить с помощью программ Дейталога. Это запросы, использующие оператор разности. Пусть заданы, например, два бинарных отношения R и S. Не существует Дейталог-правила, которое определяет отношение R-S. Тем не менее, такого рода выражения можно записать с помощью логического отрицания. И существуют расширения Дейталога, вычисляющие запросы с отрицаниями. Однако мы рассматриваем «чистый» Дейталог. Положение вещей представлено на Рисунке 3.

 

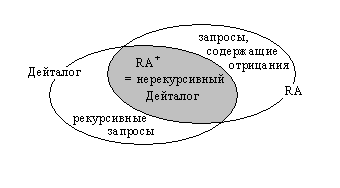
Рисунок 3

Следует отметить, что отображение программ Дейталога в уравнения RA+ позволяет использовать классические результаты, например анализ общих подвыражений и количественное определение стоимости отдельной операции реляционной алгебры.

 

Литература:

  1. Чери С., Готлоб Г., Танка Л., Логическое программирование и базы данных – М.: Мир, 1992.